Conway’s Game of Squirrels

The eastern gray squirrel (Sciurus carolinensis) is a common sight in the backyards of homes from as far north as Ontario all the way down to parts of Florida. The habitat of the gray squirrel stretches from the eastern coasts of North America to as far inland as Texas. In North America, the role played by the gray squirrel is an essential one, as they assist in the dispersal of hardwood trees. This is done via the burial of "mast," or what one typically thinks about a squirrel spending their time munching on -- acorns and other nuts. In other parts of the world, however, it is considered an invasive pest. This is because establishment of the gray squirrel in Europe has displaced native species, most notably the red squirrel (S. vulgaris). Species displacement is only one of a series of issues related to gray squirrel invasion and spread in Europe. Gray squirrels will remove the bark from trees to gnaw at the softer underlying tissue. This obviously damages trees, making them more susceptible to disease, and can make forest regeneration difficult. This concern is most prevalent in Europe, where broadleaved species such as oak and beech are most affected [1]. The gray squirrel was first introduced to England in the nineteenth century, where it would eventually spread to all of Great Britain, and it was introduced to Italy in the mid-twentieth century.

Given these detrimental ecological consequences, the gray squirrel is a suitable candidate for population control. In its native habitat, where overpopulation can have negative consequences, population control has historically taken the form of "squirrel relocation and habitat modification" [2]. Control measures in Europe are understandably less kind, and will typically take the form of "cage or kill trapping, shooting, or warfarin poisoning" [3]. Such methods have received backlash from animal rights groups, however, as was the case of a 1996 trial eradication in Italy [3]. New methods of non-lethal control have sought to circumvent these problems, with immunocontraception receiving some attention in recent decades [4,5].

A recent article in Scientific Reports considered the use of gene drives to control gray squirrel populations in the UK [6]. In this article, the authors set out the theoretical framework of a novel gene drive that is less likely to yield resistant alleles in the population and spread locally, preventing any runaway drive affects. The authors explore various scenarios with two models; one assuming random mating, and the other incorporating a spatial component. Either model employed is based on that used by Prowse et al. in [7]. In particular, Prowse et al. use a discrete-time individual-based model (IBM). The spatial model used in [6] only adds to the model in [7] by placing the population within a bounded environment (sides do not wrap around on themselves), and including distance-dependent mate allocation, offspring placement, and movement. The distance-dependent mate allocation is included by making it so that males have an exponentially decreasing probability of successful mating with a female as the distance between them increases. Offspring placement is exactly as one would expect: newly birthed individuals are placed at the location of their "mother." Regarding demography, mortality rates are assumed fixed. Finally, and most interestingly, individuals need a way of moving in the simulation. However, rather than make individuals move about the landscape randomly, individuals will only move when certain criteria are satisfied. Individual movement is density-dependent, so that individuals will only move with some probability if the density of individuals around them (in their "home range") is high enough, i.e. above some threshold. If the density is lower than this threshold, the individuals will not move. Individuals that move are referred to as "migrants," while those that stay put are "residents." The direction and distance that the migrants move are each drawn from a gamma distribution, with migrants traveling greater distances than residents.

This interesting form of movement arises from the behavior of gray squirrels in the wild. A study of gray squirrel population dynamics explored what contributed most significantly to population abundance [8]. In the introduction, the authors of [8] recount previous findings regarding gray squirrel social pressure:

Thompson (1978) describes the social system of the grey squirrel (Sciurus carolinensis). He shows that young and immigrant squirrels are subject to considerable social pressure as they attempt to establish themselves in a population. Social pressure appears to prevent establishment of the immigrants, and it was suggested that establishment of young is also affected. This suggests that dispersal, caused by intraspecific intolerance, might act to regulate population size in the grey squirrel.

Squirrels that will disperse as a result of this intraspecific aggression are referred to as "immigrants," while all other squirrels are "residents," employing a similar notation to that used in [6]. The extent of aggressive behavior that ultimately motivates dispersal is mediated by population density and the availability of resources, so that areas with greater resource abundance will tolerate a higher population density of squirrels [8]. The authors conclude with saying that "it may be speculated that the dispersal mechanism outlined in this paper is the ultimate factor regulating grey squirrel populations," [8].

Wanting to explore this further, but in a simpler manner than that used in [6,7], I opened up a fresh session of NetLogo. The simplest way I could of think of modeling this unique form of movement is with a cellular automaton, similar to Conway's Game of Life (CGOL). In fact, very similar to Conway's Game of Life, except with some important rule changes, which are discussed below:

• No density-dependent mortality. The authors of [7] explicitly do not consider density-dependent mortality as a regulating factor of the simulated squirrel population. In the original version of CGOL, cells will die if they are not surrounded by enough cells (underpopulation), or if they are surrounded by too many cells (overpopulation). These rules are relaxed.
• Density-dependent movement. How do we tell the cells to move about the environment? To accomplish this, the cells will look to their immediate environment (or "home range", represented by their Moore neighborhood) and count how many cells are occupied. If the number of cells occupying their Moore neighborhood is above some threshold, then they will move to an adjacent unoccupied cell. This certainly occurs, in contrast to the probabilistic method used in [6]. If there is no unoccupied adjacent cell, then the cells will stay put.
• Age. Death needs to occur somehow. This is accounted for by simply assigning an "age" to each cell in the simulation, representing the number of generations the cell has been alive. If the cell reaches a certain age, it will die.

The neighbor tolerance variable used in the simulation is a proxy for intraspecific aggression. Smaller values indicate greater aggression, and therefore a greater overall pressure for dispersal, resulting in rapid expansion to fill the landscape. Greater tolerances, in contrast, represent little aggression and slower dispersal across the landscape. Setting the tolerance to 8 (the maximum value) means that there is no dispersal, and all cells are technically "residents," to use the notation employed earlier. Playing around a little bit with this automaton results in some interesting emergent behavior. At times we can observe "missiles," which are similar to the "gliders" of CGOL but have a shape reminiscent of a projectile. We can observe two occurring in the simulation shown in Figure 2. All other parameters are kept the same as those used to generate the gif in Figure 1.

However, the automaton is inherently stochastic, as the cells will choose empty neighboring cells at random when moving. For example, the cluster shown in Figure 2 may sometimes produce only 1 missile if the cells move about in a different way. We can remove the randomness by setting the neighbor tolerance to its maximum value. In this case, there are no "immigrants" as the cells are fully content staying put, even if their home range is completely occupied. The illusion of movement is created by demography. Nonetheless, some interesting behavior can still be found. In Figure 3, a periodic cluster to the left is shown (reminiscent of the "blinker" in CGOL) and to the right, the pyramidal initial state eventually produces two "large missiles." Very cool stuff!

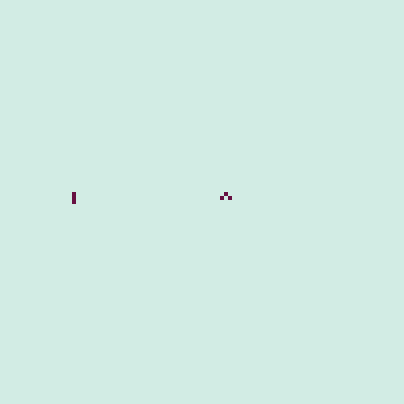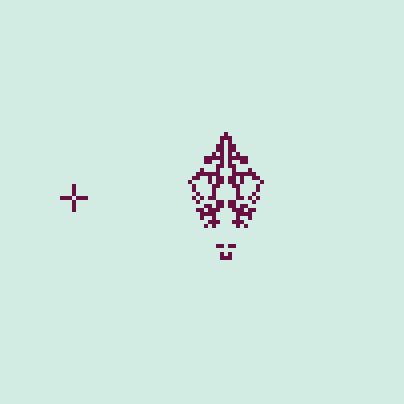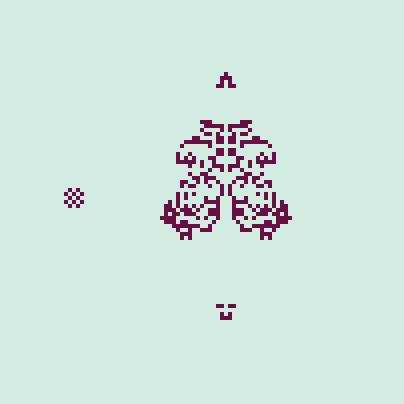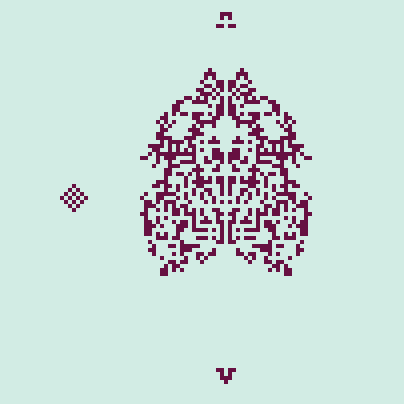
References

[1] Bruemmer, C., Lurz, P., Larsen, K., & J. Gurnell. Impacts and Management of the Alien Eastern Gray Squirrel in Great Britain and Italy: Lessons for British Columbia. Proceedings of a Conference on the Biology and Management of Species and Habitats at Risk. 1999.

[2] Hadidian, J., Manski, D., Flyger, V., Cox, C., & G. Hodge. Urban Gray Squirrel Damage and Population Management: A Case History. Third Eastern Wildlife Damage Control Conference. 1987.

[3] Sandro, B. Introduction of the American Grey Squirrel (Sciurus carolinensis) in Europe: A Case Study in Biological Invasion. Current Science. 2008; 95(7).

[4] Moore, H., Jenkins, N., & Wong, C. Immunocontraception in rodents: A Review of the Development of a Sperm-based Immunocontraceptive Vaccine for the Grey Squirrel (Sciurus carolinensis). Reproduction, fertility, and development. 1997; 9(1).

[5] Pai, M., Bruner, R., Schlafer, D., Yarrow, G., Yoder, C., & Miller, L. Immunocontraception in Eastern Gray Squirrels (Sciurus carolinensis): Morphologic Changes in Reproductive Organs. Journal of Zoo and Wildlife Medicine. 2011; 42(4).

[6] Faber, N., McFarlane, G., Gaynor, R., Pocrnic, I., Whitelaw, C, & Gorjanc, G. Novel Combination of CRISPR-based Gene Drives Eliminates Resistance and Localises Spread. Scientific Reports. 2021; 11(3719).

[7] Prowse, T., Cassey, P., Ross, J., Pfitzner, C., Wattmann, T., & Thomas, P. Dodging Silver Bullets: Good CRISPR Gene-drive Design is Critical for Eradicating Exotic Vertebrates. Proceedings of the Royal Society B. 2017; 284(1860).